Закон распределения молекул по скоростям

С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.

Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.

Чтобы лучше объяснить данный вопрос, начнем с введения такого понятия, как пространство скоростей. Оно изображено схематически на рисунке 1 .

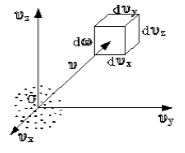
Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: «Как именно будут распределяться молекулы в пространстве скоростей»?

Очевидно, что данное распределение не будет равномерным. Если в пространстве мы выделим параллелепипед, имеющий объем d ω = d υ x d υ y d υ z , то в нем окажется d N υ молекул. Обозначим буквой N число молекул газа, тогда f ( v ) будет некоторой функцией скорости.

Распределение Максвелла

Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.

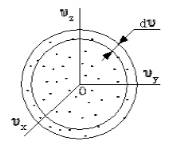
Определим, из скольких молекул состоит шаровой слой d υ . Разделим найденное выше число на количество частиц ( N ) и получим вероятность d W υ того, что пределы модуля скорости молекулы равны υ — υ + d v .

Здесь F ( v ) является функцией распределения вероятности значения v . Впервые данная функция теоретически была получена Д. Максвеллом.

Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:

d N υ = N 4 π m 0 2 πkT 3 2 e x p — m 0 υ 2 2 k T υ 2 d υ .

Здесь υ = υ x 2 + υ y 2 + υ z 2 , масса молекулы равна m 0 , а k – постоянная Больцмана.

По проекциям скоростей распределение Максвелла может быть записано так:

d N = N f υ x f υ y f υ z d υ x d υ y d υ z .

Важно учесть, что:

f υ i = m 0 2 πkT 1 2 e x p — m 0 υ i 2 2 k T ( i = x , y , z ) .

Параметры υ x , υ y , υ z означают проекции скоростей молекул на оси координат.

Также возможен следующий вариант записи распределения Максвелла:

d N = N 4 π υ v e r 3 e x p — υ υ v e r 2 υ 2 d υ .

Здесь υ υ e r обозначает наиболее вероятную скорость движения молекулы.

Как выглядит распределение Максвелла на графике

Кривая распределения молекул по скоростям на графике выглядит так:

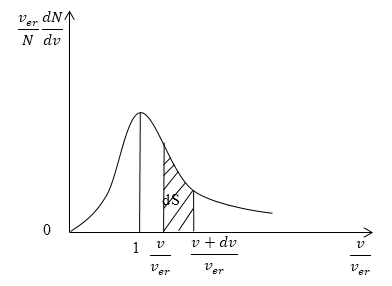
При этом доля тех молекул, которые движутся со скоростями в интервале от υ до υ + d υ будет пропорциональна площади d S , которая на графике обозначена штриховкой.

Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:

∫ 0 ∞ f ( υ ) d υ = 1 .

Оно называется условием нормировки функции распределения.

Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.

Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре Т в равновесном состоянии.

Решение

Нам потребуется распределение Максвелла (распределение по модулям скоростей).

d N υ = N 4 π m 0 2 π k T 3 2 e x p — m 0 υ 2 2 k T υ 2 d υ .

Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:

d N υ d υ = N 4 π m 0 2 πkT 3 2 2 υ υ e r e x p — m 0 υ υ e r 2 2 k T — υ υ e r 2 m 0 2 υ υ e r 2 k T e x p — m 0 υ υ e r 2 2 k T = 0 ;

2 υ υ e r — υ υ e r 2 m 0 2 υ υ e r 2 k T = 0 → 1 — υ υ e r 2 m 0 2 k T = 0 → υ υ e r 2 = 2 k T m 0 .

υ υ e r = 2 k T m 0 .

Ответ: наиболее вероятно, что скорость газа будет равна υ υ e r = 2 k T m 0 .

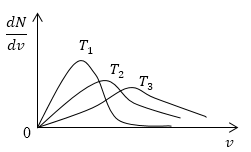
Условие: изобразите кривые распределения скоростей молекул газа при росте температуры Т .

Решение

Возьмем формулу наиболее вероятной скорости из предыдущей задачи.

υ υ e r = 2 k T m 0

Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:

Условие: дан график функции, по которой молекулы будут распределяться с учетом проекций скорости υ x . Сопоставьте количества молекул, проекции скорости которых будут принадлежать интервалам от нуля до υ x 1 и от υ x 1 до υ x 2 .

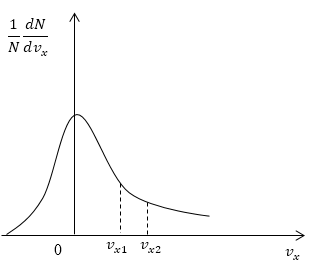
Решение

Как мы уже указывали ранее, доля молекул газа, скорости которых лежат в первом интервале, будет пропорциональна площади фигуры, образуемой кривой распределения, вертикальной осью 0 1 N d N d υ x и вертикальным пунктиром, перпендикулярным оси проекций. Во втором интервале нужная доля будет пропорциональна площади фигуры, ограниченной кривой распределения и вертикальной прямой, параллельной оси о х и проходящей через точку υ x 1 . Очевидно, что площадь первой фигуры будет меньше площади второй. Значит, и молекул, проекции скоростей которых лежат в первом интервале, будет меньше, чем во втором.

Ответ: молекул, имеющих проекции скорости в интервалах: от 0 до υ x 1 меньше, чем молекул, имеющих проекции скорости в интервалах: от υ x 1 до υ x 2 .

Закон распределения молекул по скоростям

Вы будете перенаправлены на Автор24

Закон распределения молекул по скоростям

Закон распределения молекул по скоростям описывает распределение частиц макроскопической системы при условии, что эта система находится в состоянии термодинамического равновесия, распределение является стационарным и внешние силы на систему не действуют. Данное распределение выполняется как для газов, так и жидкостей, если в них можно использовать законы классической механики.

Определить, каким образом распределены молекулы по скоростям, — это значит ответить на вопрос: «сколько молекул имеет ту или иную скорость при заданной температуре в состоянии равновесия?» Для разъяснения вопроса введем понятие: «пространство скоростей» (рис.1). В таком пространстве на декартовых осях отложены не координаты, а проекции скоростей.

В таком случае поставленный вопрос изменится на вопрос о том, как распределены молекулы в пространстве скоростей. Понятно, что молекулы распределены неравномерно.

Если в пространстве скоростей выделить параллелепипед объема $dw=dv_xdv_ydv_z$, тогда количество молекул, которые попадут в него $dN_v.$ Предположим, что N- количество молекул газа, $f(v)$- некоторая функция скорости. Тогда

Распределение Максвелла

Как было отмечено, газ находится в состоянии равновесия, все направления движения частиц равноправны, следовательно, распределение молекул в пространстве скоростей можно считать сферически симметричным (рис.2).

Найдем число молекул в шаровом слое $dv$:

Разделим (2) на число частиц (N) и найдем вероятность$ (dW_v)$ того, что модуль скорости молекулы находится в пределах от $v до v+dv$:

Готовые работы на аналогичную тему

где $Fleft(vright)$- функция распределения вероятности значения $v. $Эту функцию теоретически получил Д. Максвелл.

Таким образом, распределение молекул по скоростям (вернее их модулям) запишем как:

при этом $v=sqrt<^2+^2+^2>$, $m_0$- масса молекулы, k — постоянная Больцмана.

Можно записать распределение Максвелла по проекциям скоростей:

где $v_x,v_y,v_$ — проекции скорости молекулы на оси координат.

Еще один из вариантов написания распределения Максвелла по модулям скоростей представлен в виде:

где $v_$ — вероятнейшая скорость молекулы.

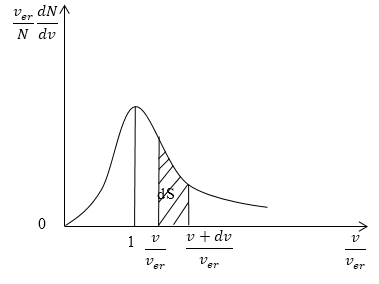
На рисунке 3 изображена кривая закона распределения молекул по скоростям. Доля молекул газа, скорости которых лежат в интервале от $v до v+dv,$ пропорциональна заштрихованной площади dS под кривой.

Поскольку скорости всех молекул лежат в интервале от $0 до+infty $, то выполняется равенство:

Это так называемое условие нормировки функции распределения.

Таким образом, распределение Максвелла зависит от массы молекулы газа и его температуры. Давление и объем в распределение не входят.

Задание: Используя распределение Максвелла, найдите наиболее вероятную скорость молекул газа в равновесном состоянии газа при температуре T.

За основу возьмем распределение молекул по модулям скоростей:

Наиболее вероятной скорости соответствует максимум функции, то продифференцируем выражение (1.1) по скорости и приравняем к нулю, получим:

Ответ: Наиболее вероятная скорость молекул газа $v_=sqrt>.$

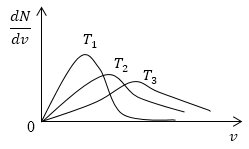
Задание: Пусть $Т_1

Из формулы для наиболее вероятной скорости молекул газа, полученной в предыдущем примере:

очевидно, что с увеличением температуры скорость растет, то есть максимум кривой смещается в сторону больших скоростей. Площадь под кривой распределения величина постоянная, следовательно, кривые изобразим следующим образом (рис.4).

Задание: На рис. 5 представлен график функции распределения молекул по проекциям скорости $v_x$. Сравнить числа молекул, имеющих проекции скорости в интервалах: от 0 до $v_$и от $v_$ до $v_$.

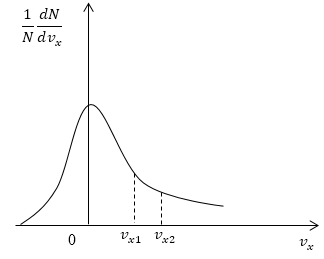
Как уже отмечалось в теоретической части, доля молекул газа, скорости которых лежат в интервале от $0 до v_,$ пропорциональна площади $S_1$ фигуры, которая ограничена кривой распределения, вертикальной осью (0$ frac<1>frac)$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей проходящей через точку $v_$. Во втором случае доля молекул газа, скорости которых лежат в интервале от $v_ до v_,$ пропорциональна площади $S_2$ фигуры, которая ограничена кривой распределения, вертикальной прямой параллельной оси (0$ frac<1>frac), проходящей через точку v_$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей, проходящей через точку $v_$. Очевидно, что $S_1>S_2. $ Следовательно, молекул, имеющих проекции скорости в интервалах: от 0 до $v_$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_$ до $v_$.

Ответ: Молекул, имеющих проекции скорости в интервалах: от 0 до $v_$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_$ до $v_$.

Закон Максвелла о распределении молекул по скоростям

Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергия и скорости отдельных молекул могут значительно отличаться от среднего значения.

С помощью теории вероятности Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.

Закон распределения Максвелла определяет относительное число молекул dN/N, скорости которых лежат в интервале (u, u + du).

Оно имеет вид:

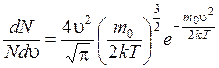(8.29)

где N – общее число молекул газа; – число молекул, скорости которых заключены в определенном интервале; u – нижняя граница интервала скоростей; du – величина интервала скоростей; T– температура газа; e = 2,718… – основание натуральных логарифмов;

k = 1,38×10 -23 Дж/К – постоянная Больцмана; m₀ – масса молекулы.

При получении этой формулы Максвелл основывался на следующих предположениях:

1. Газ состоит из большого числа N одинаковых молекул.

2. Температура газа постоянна.

3. Молекулы газа совершают тепловое хаотическое движение.

4. На газ не действуют силовые поля.

Отметим, что под знаком экспоненты в формуле (8.29) стоит отношение кинетической энергии молекулы 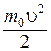к величине kT, характеризующей среднее (по молекулам) значение этой энергии.

Распределение Максвелла показывает, какая доля dN/N общего числа молекул данного газа обладает скоростью в интервале от u до u + du.

График функций распределения (рис. 8.5) асимметричен. Положение максимума характеризует наиболее часто встречающуюся скорость, которую называют наиболее вероятной скоростью u_m. Скорости, превышающие u_m, встречаются чаще, чем меньшие скорости. С повышением температуры максимум распределения сдвигается в направлении больших скоростей.

Одновременно кривая становится более плоской (площадь, заключенная под кривой, не может измениться, так как число молекул N остается постоянным).

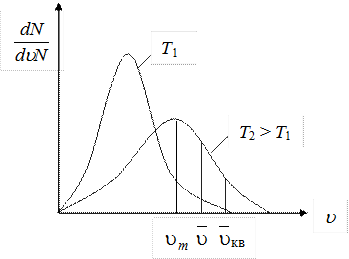
Рис. 8.5

Для определения наиболее вероятной скорости нужно исследовать на максимум функцию распределения Максвелла (приравнять первую производную к нулю и решить относительно u). В результате получаем:

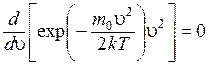Мы опустили множители, не зависящие от u. Осуществив дифференцирование, придем к уравнению:

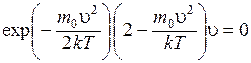Первый сомножитель (экспонента) обращается в нуль при u = ¥, а третий сомножитель (u) при u = 0. Однако из графика (рис. 8.5) видно, что значения u = 0 и u = ¥ соответствуют минимумам функции (8.29). Следовательно, значение u, отвечающее максимуму, получается из равенства нулю второй скобки: 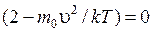. Отсюда

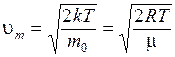. (8.30)

Введем обозначения для функции распределения молекул по скоростям (8.29):

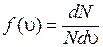. (8.31)

Известно, что среднее значение некоторой физической величины j(x) можно вычислить по формуле:

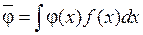. (8.32)

Из (8.32) получим выражения для среднего значения модуля скорости u и среднего значения квадрата u:

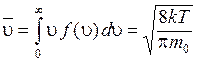, (8.33)

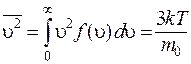. (8.34)

Таким образом, средняя скорость молекул (ее называют также средней арифметической скоростью) имеет значение:

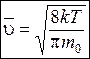. (8.35)

Квадратный корень из выражения (8.34) дает среднюю квадратичную скорость молекул:

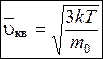. (8.36)

Отметим, что она совпадает с формулой (8.24). На рис. 8.5 приведен график функции распределения Максвелла. Вертикальными линиями отмечены три характерные скорости .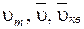

ГЛАВА 8. ЗАКОН МАКСВЕЛЛА О РАСПРЕДЕЛЕНИИ МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА ПО СКОРОСТЯМ И ЭНЕРГИЯМ

Введение

При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т.е. в любом направлении в среднем движется одинаковое число молекул.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m₀ в газе, находящемся в состоянии равновесия при Т= const, остается постоянной и равной υ_cк= .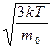

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически вывел Дж. Максвелл.

Закон Максвелла о распределении молекул идеального газа

По скоростям

При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(υ), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скоростей будет приходиться некоторое число молекул dΝ(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул 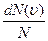, скорости которых лежат в интервале от v до υ+dυ, т.е.

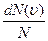=f(υ)dυ,

f(υ)= .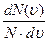

Применяя методы теории вероятностей, Максвелл нашел функцию f(υ) — закон для распределения·молекул идеального газа по скоростям:

f(υ)=4π 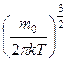υ 2 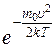. (8.1)

Из (8.1) видно, что конкретный вид функции зависит от рода газа (от массы m₀ молекулы) и от параметра состояния (от температуры T). График функции (8.1) приведен на рис.8.1.

Так как при возрастании v множитель 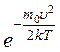уменьшается быстрее, чем растет множитель υ 2 , то функция начинаясь от нуля, достигает максимума при υ_в и затем асимптотически стремится к нулю. Кривая несимметрична относительно υ_в.

Относительное число молекул dΝ(υ)/Ν, скорости которых лежат в интервале от υ до υ+dυ, находится как площадь заштрихованной полоски. Площадь, ограниченная кривой распределения и осью абсцисс, равна 1. Это означает, что функция f(υ) удовлетворяет условию нормировки .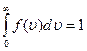

Скорость, при которой функция распределения молекул по скоростям максимальна, называется наиболее вероятной скоростьюυ_в. Значение наиболее вероятной скорости можно найти, дифференцируя выражение (8.1) (постоянные множители опускаем) по аргументу υ, приравняв результат нулю и используя условие для максимума выражения f(υ):

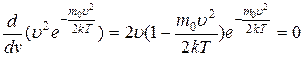Значения υ=0 и υ = ∞ соответствуют минимумам выражения (8.1), а значение υ, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость υ_в :

υ_в = 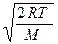= 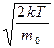. (8.2)

Из формулы (8.2) следует, что при повышении температуры максимум функции

распределения молекул по скоростям сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Средняя скорость молекулы (средняя арифметическая скорость) определяется по формуле

υ_c= _.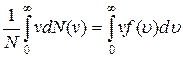

Подставляя сюда f(υ) и интегрируя, получаем:

υ_с= 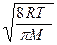= 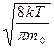. (8.3)

Скорости, характеризующие состояние газа:

– наиболее вероятная υ_в = ,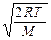

– средняя υ_с= ,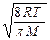

– средняя квадратичная υ_cк= .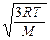

Исходя из распределения молекул по скоростям

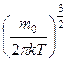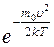dN(υ)= N f(υ)=N 4π υ 2 (8.4)

можно найти распределение молекул газа по кинетической энергии w. Для этого перейдем от переменной υ к переменной w_k = 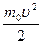. Подставив в (8.4) v= 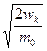и dυ=(2m₀w_k) -1/2 dw_k, получим:

dN (w)= 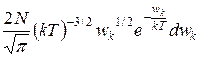= Nf(w_k)dw_k,

где dN(w_k) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от w_k до w_k+dw_k.

Таким образом, функция распределения молекул по энергиям

f(w_k)= .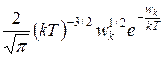

Средняя кинетическая энергия молекулы идеального газа:

w = 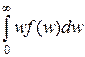= = 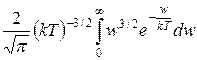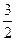kT,

т. е. получили результат, совпадающий с формулой (7.18).

Закон Максвелла о распределении молекул идеального газа по скоростям

Молекулы в газе, совершая хаотическое движение, все время сталкиваются между собой. Если предположить, как это делалось при выводе основного уравнения молекулярно-кинетической теории, что скорости молекул одинаковы, то при столкновениях молекул их скорости будут изменяться как по модулю, так и по направлению.

Если газ находится в состоянии термодинамического равновесия (Т = const), то устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Максвеллом (1859).

Максвелл при выводе распределения молекул по скоростям исходил из следующего:

1. Газ состоит из большого числа N одинаковых молекул.
2. Температура газа постоянна.
3. Молекулы газа совершают тепловое хаотическое движение.
4. Из-за хаотического движения молекул все направления движения равновероятны, т. е. в любом направлении в среднем движется одинаковое число молекул.
5. На газ не действуют силовые поля.

Если всевозможные значения скоростей

молекул разбить на малые интервалы dy, то на каждый интервал будет приходиться некоторое число молекул dN(v), скорость которых заключена в этом интервале. Функция распределения молекул по скоростям f(v) определяет

относительное число молекул —скорости которых лежат в интервале от v до v + dy, т. е.

Применяя методы теории вероятностей, Максвелл теоретически получил функцию f(v)

Как следует из выражения (6.3), при возрастании v множитель e

ло молекул скорости которых лежат в интервале от v до v + dt>, находится как площадь закрашенной полоски.

Коэффициент пропорциональности А в выражении (6.3) определяется из условия нормировки

смысл которого заключается в том, что если просуммировать все доли (относительное число) молекул со всевозможными абсолютными значениями скоростей, то получится единица.

Закон Максвелла о распределении молекул по скоростям с учетом коэффициента А:

откуда следует, что конкретный вид функции зависит от рода газа (от массы молекул) и от температуры.

Для примера на рис. 7 приведена функция распределения молекул кислорода при двух разных температурах. Как следует из рисунка, с повышением температуры максимум функции распределения молекул по скоростям смещается в сторону больших скоростей, т. е. при нагревании газа доля молекул, обладающих большими скоростями, увеличивается.

Поскольку площадь, ограниченная кривой f(v), остается постоянной (она нормируется на единицу [6.4]), то с повышением температуры (см. рис. 7) кривая распределения растягивается и понижается.

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называют наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав выражение

(6.5) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v):

Значения v = 0 и у = оо соответствуют минимумам выражения (6.5), а значение у, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость у